This article shows the feasibility of using ADC input of AVR chip as a source of True Random Number Generator (TRNG). I have prepared the testbed and recorded via UART (115200; 8N1) about 50’000’000 of 32bit random numbers. The tests took about 11 hours (including a time I spent to pray to UART for a zero-errorate). Next paragraphs describes how I made the tests. Well, just to feed the curiosity on a begining – all statistical tests failed. I was really disapointend because the generated numbers looks “fairy random”. But, the math is math.
The Testbed
When I started writing the tests I knew that the environment factors can be crucial. So, I have choose a stable, battery power supply (3x AAA, 4.5V) and adjusted the room temperature to 25°C. I also made a Farady’s box to place there a tested dev-board (with Atmega8). Only one wire (about 30cm) has been placed outside. The same wire has been connected to ADC input to emulate a floating pin with some kind of antenne to easly sniff an electronic smog. Summing up the part list – battery pack, a dev-board with ATmega8 inside secured box, a wire and stable USB-to-UART converter. That’s all.
Testing Tools
As a testing tool I choose a cool DieHarder software (random-number generator test front-end) designed by Robert G. Brown (Duke University, Physics Department). This tool is also available in Ubuntu repository.
sudo apt-get install dieharder
The DieHarder program can test generated (expectedly) random numbers using variuous test suite and also offers various pseudo random number generators. Bellow is an example of how to generate 10’000’000 random numbers using built-in PRNG and make a basic monobit test.
$ dieharder -g 0 -t 10000000 -o -f test.dat
$ dieharder -d 100 -g 202 -f test.dat
#=============================================================================#
# dieharder version 3.31.1 Copyright 2003 Robert G. Brown #
#=============================================================================#
rng_name | filename |rands/second|
file_input| test.dat| 5.04e+06 |
#=============================================================================#
test_name |ntup| tsamples |psamples| p-value |Assessment
#=============================================================================#
# The file file_input was rewound 2 times
sts_monobit| 1| 100000| 100|0.02678203| PASSED
A list of tests available
$ dieharder -l #=============================================================================# # dieharder version 3.31.1 Copyright 2003 Robert G. Brown # #=============================================================================# Installed dieharder tests: Test Number Test Name Test Reliability =============================================================================== -d 0 Diehard Birthdays Test Good -d 1 Diehard OPERM5 Test Good -d 2 Diehard 32x32 Binary Rank Test Good -d 3 Diehard 6x8 Binary Rank Test Good -d 4 Diehard Bitstream Test Good -d 5 Diehard OPSO Suspect -d 6 Diehard OQSO Test Suspect -d 7 Diehard DNA Test Suspect -d 8 Diehard Count the 1s (stream) Test Good -d 9 Diehard Count the 1s Test (byte) Good -d 10 Diehard Parking Lot Test Good -d 11 Diehard Minimum Distance (2d Circle) Test Good -d 12 Diehard 3d Sphere (Minimum Distance) Test Good -d 13 Diehard Squeeze Test Good -d 14 Diehard Sums Test Do Not Use -d 15 Diehard Runs Test Good -d 16 Diehard Craps Test Good -d 17 Marsaglia and Tsang GCD Test Good -d 100 STS Monobit Test Good -d 101 STS Runs Test Good -d 102 STS Serial Test (Generalized) Good -d 200 RGB Bit Distribution Test Good -d 201 RGB Generalized Minimum Distance Test Good -d 202 RGB Permutations Test Good -d 203 RGB Lagged Sum Test Good -d 204 RGB Kolmogorov-Smirnov Test Test Good -d 205 Byte Distribution Good -d 206 DAB DCT Good -d 207 DAB Fill Tree Test Good -d 208 DAB Fill Tree 2 Test Good -d 209 DAB Monobit 2 Test Good
A list of generators (PRNG)
$ dieharder -g -l #=============================================================================# # dieharder version 3.31.1 Copyright 2003 Robert G. Brown # #=============================================================================# # Id Test Name | Id Test Name | Id Test Name # #=============================================================================# | 000 borosh13 |001 cmrg |002 coveyou | | 003 fishman18 |004 fishman20 |005 fishman2x | | 006 gfsr4 |007 knuthran |008 knuthran2 | | 009 knuthran2002 |010 lecuyer21 |011 minstd | | 012 mrg |013 mt19937 |014 mt19937_1999 | | 015 mt19937_1998 |016 r250 |017 ran0 | | 018 ran1 |019 ran2 |020 ran3 | | 021 rand |022 rand48 |023 random128-bsd | | 024 random128-glibc2 |025 random128-libc5 |026 random256-bsd | | 027 random256-glibc2 |028 random256-libc5 |029 random32-bsd | | 030 random32-glibc2 |031 random32-libc5 |032 random64-bsd | | 033 random64-glibc2 |034 random64-libc5 |035 random8-bsd | | 036 random8-glibc2 |037 random8-libc5 |038 random-bsd | | 039 random-glibc2 |040 random-libc5 |041 randu | | 042 ranf |043 ranlux |044 ranlux389 | | 045 ranlxd1 |046 ranlxd2 |047 ranlxs0 | | 048 ranlxs1 |049 ranlxs2 |050 ranmar | | 051 slatec |052 taus |053 taus2 | | 054 taus113 |055 transputer |056 tt800 | | 057 uni |058 uni32 |059 vax | | 060 waterman14 |061 zuf | | #=============================================================================# | 200 stdin_input_raw |201 file_input_raw |202 file_input | | 203 ca |204 uvag |205 AES_OFB | | 206 Threefish_OFB |207 XOR (supergenerator)|208 kiss | | 209 superkiss | | | #=============================================================================# | 400 R_wichmann_hill |401 R_marsaglia_multic. |402 R_super_duper | | 403 R_mersenne_twister |404 R_knuth_taocp |405 R_knuth_taocp2 | #=============================================================================# | 500 /dev/random |501 /dev/urandom | | #=============================================================================# #=============================================================================#
Software
Testing Software for ATmega8 (slow)
Bellow is a testing software for ATmega8 (@16MHz) which produces a specified amount of (expectedly) random numbers and sends via UART (as a text) using Die Harder format. It’s a very slow version to demonstrate only an idea how to make a test and allow to play with the resulting data. The data can be read with any serial tool – i.e. CuteCom.
The bit-stream algorithm uses a least significant bit of ADC value. Also tested with alogrithm using two least significant bits of ADC value.
#include <stdint.h>
#include <avr/io.h>
#include <avr/interrupt.h>
#define N (32UL) // number of bits
#define SAMPLES (1000UL)
#define BAUDRATE (115200UL)
static uint8_t data[N];
volatile uint8_t counter = 0;
static void ADCRNG_init(void);
static uint32_t ADCRNG_next(void);
static void UART_init(uint32_t baudrate);
static void UART_putc(char c);
static void UART_puts(const char *s);
static void UART_putu32(uint32_t v);
int
main(void) {
uint32_t random, n;
ADCRNG_init(); // initialize ADCRNG
UART_init(BAUDRATE); // initialize UART
sei(); // enable global interrupts
UART_puts("type: d\n");
UART_puts("count: "); UART_putu32(SAMPLES); UART_putc('\n');
UART_puts("numbit: "); UART_putu32(N); UART_putc('\n');
for (n = 0; n < SAMPLES; ++n) {
random = ADCRNG_next(); // get the random number
UART_putu32(random); // and send it via serial port
UART_putc('\n');
}
while(1); // infinite loop
}
ISR(ADC_vect) {
if (counter < N) {
data[counter++] = ADCH; // store ADC value
ADCSRA |= _BV(ADSC); // run next signal acquisition
}
}
void ADCRNG_init(void) {
ADMUX |= _BV(REFS0)|_BV(REFS0); // use internal 2.56V voltage reference
ADMUX |= _BV(ADLAR); // set left adjustment of ADC result (8bit mode)
ADCSRA = _BV(ADPS1)|_BV(ADPS0); // set division factor to 2
ADCSRA |= _BV(ADEN)|_BV(ADIE); // enable ADC0 (interrupt)
}
uint32_t ADCRNG_next(void) {
uint8_t i;
uint32_t result = 0;
counter = 0; // reset counter
ADCSRA |= _BV(ADSC); // start signal acquisition
while (counter != N); // wait for data
for (i = 0; i < N; ++i, result <<= 1) {
result |= (data[i] & 1); // use least significant bit
}
return result;
}
void UART_init(uint32_t baudrate) {
uint16_t baudrate_calc = (F_CPU / 4 / baudrate - 1) / 2;
DDRD |= _BV(PD1); // set PD1 (TXD) as output
UBRRH = baudrate_calc >> 8; // set calculated baudrate, high
UBRRL = baudrate_calc; // and low register
UCSRA = _BV(U2X); // double the transmition speed
UCSRB = _BV(TXEN); // enable transmission
UCSRC = _BV(URSEL)|(1<<UCSZ1)|(1<<UCSZ0); // set format 8N1
}
void UART_putc(char c) {
while (!(UCSRA & _BV(UDRE))); // wait for empty buffer
UDR = c; // put data into buffer
}
void UART_puts(const char *s) {
while (*s) UART_putc(*(s++));
}
void UART_putu32(uint32_t v) {
char buff[11];
char *p = buff + 10; // switch to end of buffer
*p = 0; // set string null-termination
do {*(--p) = (v % 10L) + '0'; v /= 10L;} while (v); // convert
UART_puts((const char *)p);
}
Testing Software for ATmega8 (fast)
Bellow is another testing software for ATmega8 (@16MHz) which produces a specified amount of random numbers and sends it via UART (as a binary). It’s a very similar (different only inside main function) but fast version which does not use Die Harder format. It simply sends number of samples (as a text) and then random numbers as binary data. The data can be read with the attached python script. The script reads the data from serial port and converts the bit stream to text version of Die Harder format.
int
main(void) {
uint32_t random, n;
char *p;
ADCRNG_init(); // initialize ADCRNG
UART_init(BAUDRATE); // initialize UART
sei(); // enable global interrupts
UART_putu32(SAMPLES); UART_putc('\n'); // print number of samples
for (n = 0; n < SAMPLES; ++n) {
random = ADCRNG_next(); // get the random number
p = (char *)&random;
UART_putc(p[0]); // send the 4byte integer via UART
UART_putc(p[1]);
UART_putc(p[2]);
UART_putc(p[3]);
}
while(1); // infinite loop
}
Python script to read binary data
A python (>=2.7) script to read a data from serial port and convert the bit-stream to Die Harder text format.
#!/bin/env python
import serial
import struct
with serial.Serial('/dev/ttyUSB0', 115200, timeout=100) as s:
line = s.readline()
n = int(line)
print("type: d")
print("count: {}".format(n))
print("numbit: 32")
while n > 0:
data = s.read(4);
sample = struct.unpack("<I", data)[0]
print("%10d" % sample)
n -= 1
Testing Procedure
- Record 4’000’000 samples,
- run DieHarder tests,
- repeat (10 times).
Example Test Results
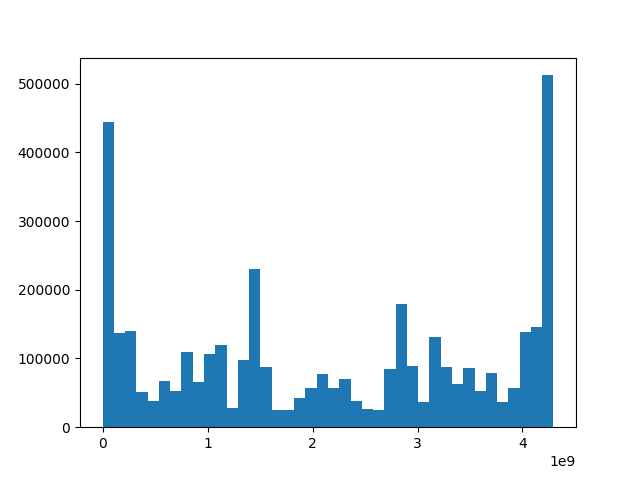
Histogram describing uniformity of distribution of tested random numbers (test4m1.log, ~44MB). As you can see the distribution of the numbers is not regular.
DieHarder output.
$ dieharder -a -g 202 -f test4m1.log
#=============================================================================#
# dieharder version 3.31.1 Copyright 2003 Robert G. Brown #
#=============================================================================#
rng_name | filename |rands/second|
file_input| test4m1.log| 4.90e+06 |
#=============================================================================#
test_name |ntup| tsamples |psamples| p-value |Assessment
#=============================================================================#
# The file file_input was rewound 3 times
diehard_birthdays| 0| 100| 100|0.00000000| FAILED
# The file file_input was rewound 28 times
diehard_operm5| 0| 1000000| 100|0.00000000| FAILED
# The file file_input was rewound 60 times
diehard_rank_32x32| 0| 40000| 100|0.00000000| FAILED
# The file file_input was rewound 75 times
diehard_rank_6x8| 0| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 82 times
diehard_bitstream| 0| 2097152| 100|0.00000000| FAILED
# The file file_input was rewound 134 times
diehard_opso| 0| 2097152| 100|0.00000000| FAILED
# The file file_input was rewound 169 times
diehard_oqso| 0| 2097152| 100|0.00000000| FAILED
# The file file_input was rewound 185 times
diehard_dna| 0| 2097152| 100|0.00000000| FAILED
# The file file_input was rewound 187 times
diehard_count_1s_str| 0| 256000| 100|0.00000000| FAILED
# The file file_input was rewound 219 times
diehard_count_1s_byt| 0| 256000| 100|0.00000000| FAILED
# The file file_input was rewound 219 times
diehard_parking_lot| 0| 12000| 100|0.00000000| FAILED
# The file file_input was rewound 220 times
diehard_2dsphere| 2| 8000| 100|0.00000000| FAILED
# The file file_input was rewound 220 times
diehard_3dsphere| 3| 4000| 100|0.00000000| FAILED
# The file file_input was rewound 261 times
diehard_squeeze| 0| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 261 times
diehard_sums| 0| 100| 100|0.00000000| FAILED
# The file file_input was rewound 264 times
diehard_runs| 0| 100000| 100|0.00000000| FAILED
diehard_runs| 0| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 294 times
diehard_craps| 0| 200000| 100|0.00000000| FAILED
diehard_craps| 0| 200000| 100|0.00000000| FAILED
# The file file_input was rewound 794 times
marsaglia_tsang_gcd| 0| 10000000| 100|0.00000000| FAILED
marsaglia_tsang_gcd| 0| 10000000| 100|0.00000000| FAILED
# The file file_input was rewound 797 times
sts_monobit| 1| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 799 times
sts_runs| 2| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 802 times
sts_serial| 1| 100000| 100|0.00000000| FAILED
sts_serial| 2| 100000| 100|0.00000000| FAILED
sts_serial| 3| 100000| 100|0.00000000| FAILED
sts_serial| 3| 100000| 100|0.00000000| FAILED
sts_serial| 4| 100000| 100|0.00000000| FAILED
sts_serial| 4| 100000| 100|0.00000000| FAILED
sts_serial| 5| 100000| 100|0.00000000| FAILED
sts_serial| 5| 100000| 100|0.00000000| FAILED
sts_serial| 6| 100000| 100|0.00000000| FAILED
sts_serial| 6| 100000| 100|0.00000000| FAILED
sts_serial| 7| 100000| 100|0.00000000| FAILED
sts_serial| 7| 100000| 100|0.00000000| FAILED
sts_serial| 8| 100000| 100|0.00000000| FAILED
sts_serial| 8| 100000| 100|0.00000000| FAILED
sts_serial| 9| 100000| 100|0.00000000| FAILED
sts_serial| 9| 100000| 100|0.00000000| FAILED
sts_serial| 10| 100000| 100|0.00000000| FAILED
sts_serial| 10| 100000| 100|0.00000000| FAILED
sts_serial| 11| 100000| 100|0.00000000| FAILED
sts_serial| 11| 100000| 100|0.00000000| FAILED
sts_serial| 12| 100000| 100|0.00000000| FAILED
sts_serial| 12| 100000| 100|0.00000000| FAILED
sts_serial| 13| 100000| 100|0.00000000| FAILED
sts_serial| 13| 100000| 100|0.00000000| FAILED
sts_serial| 14| 100000| 100|0.00000000| FAILED
sts_serial| 14| 100000| 100|0.00000000| FAILED
sts_serial| 15| 100000| 100|0.00000000| FAILED
sts_serial| 15| 100000| 100|0.00000000| FAILED
sts_serial| 16| 100000| 100|0.00000000| FAILED
sts_serial| 16| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 807 times
rgb_bitdist| 1| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 817 times
rgb_bitdist| 2| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 832 times
rgb_bitdist| 3| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 852 times
rgb_bitdist| 4| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 877 times
rgb_bitdist| 5| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 907 times
rgb_bitdist| 6| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 942 times
rgb_bitdist| 7| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 982 times
rgb_bitdist| 8| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 1027 times
rgb_bitdist| 9| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 1077 times
rgb_bitdist| 10| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 1132 times
rgb_bitdist| 11| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 1192 times
rgb_bitdist| 12| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 1197 times
rgb_minimum_distance| 2| 10000| 1000|0.00000000| FAILED
# The file file_input was rewound 1204 times
rgb_minimum_distance| 3| 10000| 1000|0.00000000| FAILED
# The file file_input was rewound 1214 times
rgb_minimum_distance| 4| 10000| 1000|0.00000000| FAILED
# The file file_input was rewound 1227 times
rgb_minimum_distance| 5| 10000| 1000|0.00000000| FAILED
# The file file_input was rewound 1232 times
rgb_permutations| 2| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 1239 times
rgb_permutations| 3| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 1249 times
rgb_permutations| 4| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 1262 times
rgb_permutations| 5| 100000| 100|0.00000000| FAILED
# The file file_input was rewound 1287 times
rgb_lagged_sum| 0| 1000000| 100|0.00000000| FAILED
# The file file_input was rewound 1337 times
rgb_lagged_sum| 1| 1000000| 100|0.00000000| FAILED
# The file file_input was rewound 1412 times
rgb_lagged_sum| 2| 1000000| 100|0.00000000| FAILED
# The file file_input was rewound 1512 times
rgb_lagged_sum| 3| 1000000| 100|0.00000000| FAILED
# The file file_input was rewound 1637 times
rgb_lagged_sum| 4| 1000000| 100|0.00000000| FAILED
# The file file_input was rewound 1787 times
rgb_lagged_sum| 5| 1000000| 100|0.00000000| FAILED
# The file file_input was rewound 1962 times
rgb_lagged_sum| 6| 1000000| 100|0.00000000| FAILED
# The file file_input was rewound 2162 times
rgb_lagged_sum| 7| 1000000| 100|0.00000000| FAILED
Final Words
According to the tests have been made the myth has been refuted! ADC of AVR chips has not enough entropy to build TRNG (True Random Number Generator). However, it has enough randomness to generate seed numbers for PRNG (Pseudo Random Number Generator).
Dosuwając wynik do lewej i odrzucając dwa najmłodze bity odfiltrowałeś szum. A więc już na starcie test utracił wartość poznawczą. Sugeruję powtórzenie testu na 10 bitowej wartości.
Sławku, chyb nie rozumiem Twojej sugestii. Zmienna wynikowa (result) jest składana właśnie z potencjalnie losowych, najmłodszych bitów odczytanych z ADC. Wspomniane przesunięcie służy tylko do zrobienia miejsca na kolejny bit.
Co do użycia 10 bitowej wartości ADC to również to testowałem i w tym eksperymencie rozkład wypadał dużo gorzej :/ Układ ma kilka punktów swobody – być może inny zestaw dałby lepsze/gorsze wyniki.
/L
W tej konfiguracji w rejestrze ACDH lądują bity od nr 2 do 9, bity 0 i 1, a więc najmłodsze są odrzucane. I o to mi chodzi.
Ale OK, zrobiłem test na 10 bitach i też wyszło słabo :-/
W każdym razie dzięki za poruszenie tematu i rozwianie mitu straszącego po internetach.
I recently made an RNG using an STM32 which does not come with an hardware RNG(some do).
I used the internal temperature sensor as a source for entropy (WDT is a possible candidate too).
The key is not to use your entropy source directly but to feed it through a randomness extractor. A randomness extractor should produce a random number if you feed enough bits to it with enough entropy even if there is some correlation. What you did is treat 1 adc bit as 1 random bit. But the adc-bits are not random. They are correlated since the ratio of 1’s and 0’s is not 1:1 and the spectrum may not be flat. I would be cautious to use a floating input as a source since you are depended on what radiowaves are present and without a nyquist filter you are guaranteed to get frequency folding. Some people use diodes as a source of noise.
I noticed my ADC values only varied about 7*lsb values most of the time and there were a lot of 2-lsb jumps in my data. So I decided not to use only 1 bit but the lowest 4 bits since I did not want to throw out any entropy.
I used fourier to check the spectrum. I used a histogram to check values. The spectrum looked ok, no strong peaks (with the exception of an obvious dc offset). The histogram followed a nice bell curve, not a flat distribution, but that is fine!
I packed 2 4-bit samples in one byte. I fed 128 samples (64 bytes) to a crc32 function which should have plenty of randomness for 32-bit values, even if the entropy is only 1/4 bit per sample.
I generated 10M values and it passed most dieharder tests. Using numbers generated by dieharder itself produced the same result.
To save execution time I only use it as a seed value in my code.
If I had more time I would reduce the number of samples fed into the crc-function until the tests start failing. This way I would know now much entropy it generates.
Hi Chris,
thanks for leaving this valuable note. I was delighted reading your experience of making a RNG on STM32. I hope to find more time for this experiment to try to get a better distribution result with diode as source of the noise.
Take Care
/LP
I appreciate the effort to this study. -I’d like a true random number generator for a project I’m working on. Looking the documentation over, I end up with theories and questions:
1. Geometry of “pick-up”.. -Was a different length tried? Was the test done indoors/outdoors? Was the “antenna” vertical or, horizontal?
2. Any amplification? Truly small signals may get swamped by adjacent circuitry on the processor (which might account for the four “lobes” in the graph).
3. If “Thermal Background Noise” is random enough, I think I’d just connect the ADC pin to a diode biased at it’s “knee”. (My simplest suggestion..)
Hi Matthew, thanks for asking this questions.
1. The wire length was the same for all test runs. Also, the a wire was laying down on the kitchens (wooden) table top.
2. No amplification. My intention was to check ADC without extra components. Probably will give better result.
3. Yes, diode connected in series with an “antenna” wire have a better result (much much better). I run some extra tests with a diode as well. Entropy is higher but distribution is still poor. Anyway, it also failed all statistical tests. It’s an experience I forgot to share. But thanks to you I will leave it here, in a comment.
If you would like a file with samples from test with diode I still have it and I can share it via email.
/L